
In simple terms, any object when laid over its other counterpart appears to be the same figure or Xerox copies of each other are congruent. Though the triangles will have the same shape and size, one will appear as a mirror image of the other. So, what are congruent triangles? Triangles are said to be in congruence when every corresponding side and interior angles are congruent (of the same length).

The common variants are isosceles, equilateral, scalene, etc. Some time placed here makes teaching the cases of the Law of Sines later much easier because some student already understand the ambiguous case.As a plane enclosed figures with 3-sides, segments - “triangles” are of different types based upon their sides and angles. I find that introducing the ‘swinging side’ opens their eyes to non-congruent cases. It is natural and isn’t too much to bite off. I do discuss the cases of ASS here when teaching an honors class. They recognized right away that the side held things in check and at least one side was necessary for congruence. Going from AA to ASA, was a very clear moment for them. They quickly could see what things were needed to 'lockdown' the shape. I created an exploration where students create triangle based on certain criteria and then they compare (map) their triangles with a group. Triangles being the simplest polygon appear everywhere and their properties and correspondence of congruent parts unlock many geometric mysteries.

Knowing when two triangles are congruent is essential to so many areas that follow. The definitions and the composite transformations will link isometry to congruence.
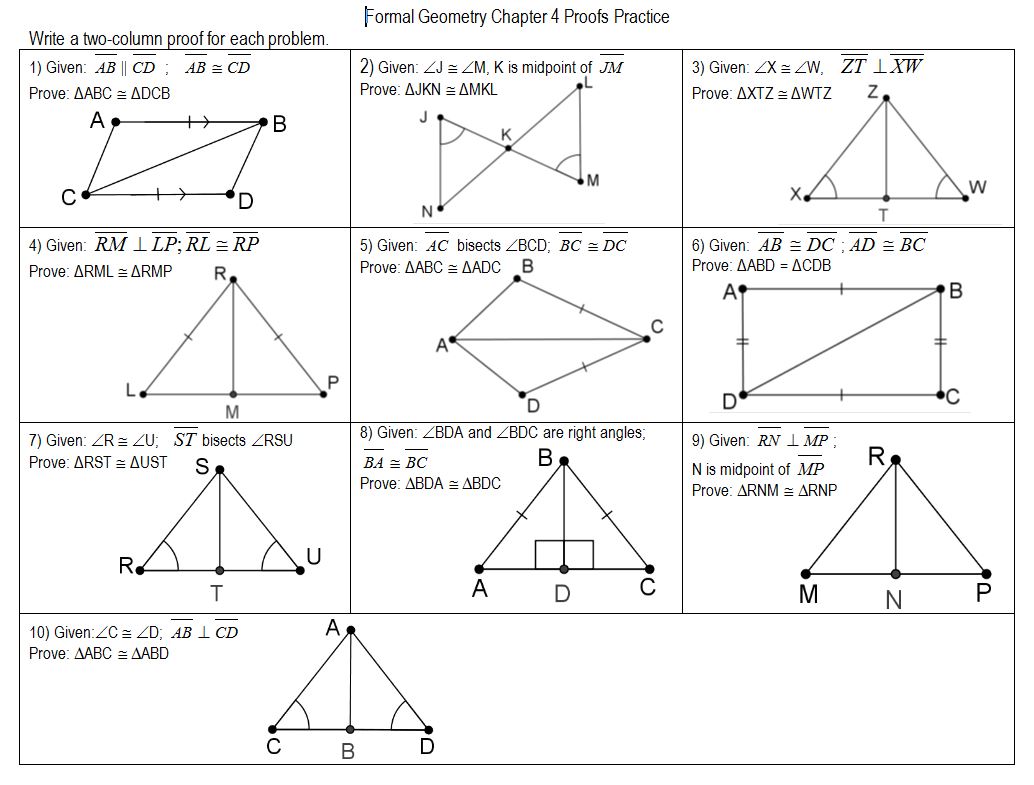
Students will use the concepts covered in G.CO.4 and G.CO.5. I have them label an S or an A on the diagram and I talk about how you must know the next side or the next consecutive angle to continue naming in that direction… if not. Students often ask about where to start when naming the criteria… this can be difficult at first to see. Students confuse AAS with ASA quite a bit, they struggle to determine if the side is between the angles or not. The most difficult part of this is the correct ordering of the sides and angles. Determining and then applying the minimal criteria for congruence saves us time and makes us more efficient. (2) The student will be able to explain in what cases AA and ASS do and don't prove triangle congruency.ĭue to the simplicity of the triangle, the criteria for congruence does not have to be knowing 3 congruent corresponding sides and 3 congruent corresponding angles.

(1) The student will be able to explain and apply the criteria of SSS, SAS, ASA, AAS, and HL to prove triangle congruency. Doing so will greatly help them when you work on the ambiguous cases of the Sine Law. I also believe that if you are teaching Honors Geometry you need to discuss the cases of ASS at this point. I believe that these also need to be investigated and integrated into this objective. Notice that AAS and HL are not mentioned here. This investigatory approach is essential to the development of this concept. That means we are to create triangles with certain characteristics and then see if one maps onto the other. It is important to note how the objective tells us to arrive at those criteria through our definition of congruence in terms of rigid motion. This objective focuses on the development of the minimal criteria needed to determine congruence between two triangles. High School Geometry Common Core G.CO.B.8 - Congruence Criteria - PattersonĮxplain how the criteria for triangle congruence (ASA, SAS, and SSS) follow from the definition of congruence in terms of rigid motion.


 0 kommentar(er)
0 kommentar(er)
